Goal of Machine Learning

Machine Learning or Deep Learning can be viewed as function approximation based on data. What this means in simpler terms is that given a set of data points the aim is to get a function that can represent each of the data point very well and this function generalizes across many such similar data points.

A simple polynomial curve fitting example is shown below. The idea of machine learning is to achieve something similar to left bottom figure so that there is a little bit of generalization or extrapolation that can be done if a sample comes from similar distribution.

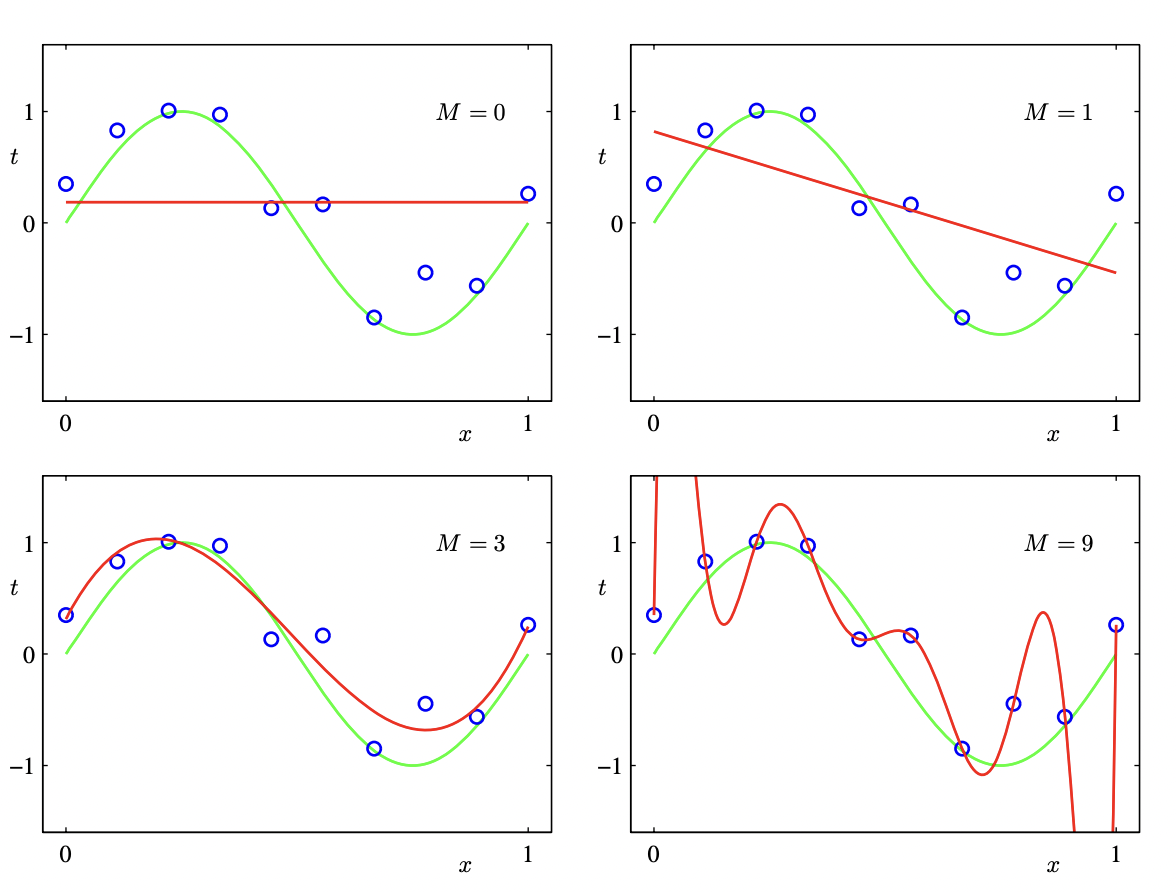Function Approximation [1]

In case of the first diagram

Loss Function

Loss function is the function that can depict the error between the predicted function value at a data point and the actual value. Loss functions are measured over single datum points.

Cost Function

Cost function also denotes the error between predicted value and actual value but for a batch of data values.

Mathematical properties of Loss Function

For a loss function these mathematical properties are important

  • Differentiable in real domain completely
  • Possibly convex to ensure that there is a minimum, but in case of deep learning the loss function landscape will generally not be convex and we will have to do with the local minimum.

Common Loss Functions

  • Cross Entropy Loss

Cross entropy loss is generally used for classification problems and can be expressed mathematically as

  1. Multi label classification
\[L = \frac{1}{m} \sum_{i=1}^{m} y_i log(\hat{y}_i)\]
  1. Binary classification
\[L = \frac{1}{m} \sum_{i=1}^{m} (y_i log(\hat{y}_i) + (1 - y_i log(1 - \hat{y}_i)))\]

where $y_i$ represents the label and $\hat{y}_i$ is the prediction for $m $ samples

  • Hinge Loss

This loss function was developed for the SVM classification methods

\[L = max(0, 1 - y* f(x))\]
  • Mean Squared Error

Mean Squared error is generally used for regression based problems and can be represented mathematically as

\[L = \frac {\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{n}\]

Basically computes the distance between the sample and prediction and then averages it over n samples

  • Adversarial Loss function

Adversarial Loss is used in case Generative Adversarial networks where the discriminator and generator fight a zero sum game against each other.

\[\min_{G}\max_{D}\mathbb{E}_{x\sim p_{\text{data}}(x)}[\log{D(x)}] + \mathbb{E}_{z\sim p_{\text{z}}(z)}[1 - \log{D(G(z))}]\]

where G is the Generator and D is the discriminator

References

  1. Figure 1.4, Pattern Recognition and Machine Learning, Christoher Bishop